Besaran skalar adalah besaran yang hanya memiliki besaran dan cukup dinyatakan dengan sebuah angka dan sebuah satuan. Lambang suatu besaran skalar dicetak dengan huruf miring, misalnya (m = massa, t = waktu, V = volume).
Besaran vektor adalah besaran yang selain memiliki besar (nilai) juga memiliki arah. Lambang suatu besaran vektor dicetak dengan huruf tegak cetak tebal (v = kecepatan, F = gaya, s = perpindahan) dan jika ditulis tangan dinyatakan dengan anak panah di atas lambang besaran. Besaran vektor dinotasikan dengan sebuah anak panah (lihat gambar di bawah), di mana panjang anak panah menunjukkan besar vektor (5 cm) dan arah anak panah menunjukkan arah vektor. Arah vektor biasa dinyatakan dengan besar sudut terhadap arah acuan tertentu, misalnya 30o terhadap horizontal.
Adapun sifat-sifat vektor yaitu :
- Sifat komutatif : A + B = B + A
- Sifat asosiatif : A + (B + C) = (A + B)C
- α(A + B) = αA + αB
- |A| + |B| ≥ |A + B|
- Dua vektor dikatakan sama (A = B) apabila kedua vektor tersebut memiliki panjang dan arah yang sama
- Vektor negatif (-A) adalah vektor yang panjangnya sama dengan panjang (A) tetapi arahnya berlawanan dengan arah (A)
- kA adalah vektor yang panjangnya k kali panjang A, dengan arah yang sama dengan A jika k positif, dan berlawanan dengan A jika k negatif
- Suatu vektor dapat digeser tanpa mengubah sifat-sifatnya apabila besar dan arah vektornya masih sama.
- Jika nilai k adalah +2, besar kA yaitu dua kali besar A dengan arah yang tetap yaitu ke kanan
- Jika nilai k adalah -2, besar kA juga dua kali besar A namun arahnya berlawanan dengan A yaitu ke kiri
Vektor A memiliki besar dan arah yang sama dengan vektor B, sehingga kedua vektor dapat dikatakan sama (A = B).
Vektor A memiliki besar yang sama dengan vektor A, namun memiliki arah yang berlawanan, sehingga kedua vektor tersebut dikatakan tidak sama (A ≠ -A).
Vektor satuan adalah suatu vektor yang besarnya satu satuan. Pada diagram cartesius terdapat 3 vektor satuan yaitu :
i → vektor
satuan sumbu X
j → vektor
satuan sumbu Y
k → vektor
satuan sumbu Z
B. Operasi Vektora. Resultan Vektor
Resultan Vektor didefinisikan sebagai penjumlahan besaran-besaran vektor. Ketika menjumlahkan besaran-besaran vektor, arah vektor harus diperhatikan. Resultan dua buah vektor V1 dan V1 yang membentuk sudut apit α dapat dihitung menggunakan persamaan :

Untuk menentukan arah resultan vektor, terhadap salah satu vektor penyusunnya, dapat digunakan persamaan sinus sebagai berikut :
Ada beberapa metode dalam operasi penjumlahan vektor yaitu :
- Metode segitiga
Untuk menjumlahkan dua buah vektor secara segitiga, maka :
- Lukislah vektor A terlebih dahulu dengan besar dan arah yang sama
- Lukislah vektor B dengan pangkal (ekor) B berada di ujung (kepala) A dengan besar dan arah yang sama pula
- Lukislah garis vektor dari pangkal (ekor) A hingga ujung (kepala) B sebagai vektor resultan (R), sehingga pangkal (ekor) R akan berimpit dengan pangkal (ekor) A, dan ujung (kepala) R akan berimpit dengan ujung (kepala) B
2. Metode poligon
Metode poligon pada dasarnya sama dengan metode segitiga, namun metode poligon digunakan pada penjumlahan lebih dari dua vektor. Vektor-vektor tersebut digambar sambung-menyambung kepala-ekor (perhatikan panjang dan arah vektor harus dilukis dengan tepat), dan resultan R adalah vektor yang menghubungkan ekor vektor yang pertama dengan ekor vektor yang terakhir.
Untuk menjumlahkan beberapa vektor secara poligon yaitu :
- Lukislah A terlbih dulu dengan besar dan arah yang sama
- Lukislah B dengan pangkal (ekor) B berada di ujung (kepala) A dengan besar dan arah yang sama pula
- Lukislah C dan D sama seperti melukis B
- Lukislah garis vektor dari pangkal (ekor) A hingga ujung (kepala) D sebagai vektor resultan (R), sehingga pangkal (ekor) R akan berimpit dengan pangkal (ekor) A, dan ujung (kepala) R akan berimpit dengan ujung (kepala) D
3. Metode Jajargenjang
Untuk menjumlahkan dua buah vektor secara jajargenjang, resultan dua vektor yang berpotongan adalah diagonal jajargenjang dengan kedua vektor tersebut sebagai sisi jajargenjang, dan ekor resultan R berimpit dengan ekor kedua vektor tersebut.
Untuk melakukan penjumlahan vektor secara jajargenjang yaitu :
- Lukislah vektor pertama dan kedua dengan titik pangkal berimpit
- Lukis sebuah jajargenjang dengan kedua vektor tersebut sebagai sisi-sisinya
- Diagonal jajargenjang yang titik pangkalnya sama dengan titik pangkal kedua vektor adalah merupakan resultan vektor
Contoh soal :
Dua buah vektor P dan Q saling membentuk sudut 60o . Jika besar kedua vektor tersebut berturut-turut adalah 60 N dan 40 N, tentukanlah besar dan arah resultan kedua vektor terhadap vektor Q!
Pembahasan :
Diketahui : kedua vektor dapat digambarkan sebagai berikut

Ditanyakan : besar dan arah resultan (R) ....?
Dijawab :
4. Metode Analitis
Untuk melakukan penjumlahan vektor secara analitis, langkah-langkah yang harus dilakukan yaitu sebagai berikut :
- Tentukan besar setiap komponen vektor pada sumbu X dan pada sumbu Y
- Tentukan besar resultan vektor-vektor pada sumbu X dan Y
- Tentukan besar dan arah resultan
Selisih vektor disebut juga sebagai pengurangan vektor. Jika vektor C adalah selisih vektor A dan vektor B, maka :
Besar vektor C adalah
Selisih antara dua buah vektor A dan B (ditulis R = A – B) sama saja dengan menentukan jumlah antara vektor A dengan vektor –B atau R = A + (-B). Oleh karena itu, tiga metode dalam penjumlahan vektor yang telah dipelajari sebelumnya juga berlaku untuk selisish vektor. Untuk melukiskan R = A – B, mula-mula lukislah A, kemudian lukis juga –B dengan berlawanan arah dengan B.
c. Perkalian Vektor
- Perkalian titik vektor (dot product)
(i.i = j.j = k.k = 1)
Dan sama dengan nol jika keduanya tidak sejenis
(i.j = j.k = k.i = 0)
Perkalian titik dua buah vektor akan menghasilkan sebuah besaran skalar. Jenis perkalian ini bersifat komutatif.
- Perkalian silang vektor (cross product)
Hasil perkalian silang antara dua vektor satuan yang sejenis sama dengan nol
i.i = j.j = k.k = 0
Perkalian silang dua vektor satuan tidak sejenis ditentukan oleh diagram lingkaran putar kiri (berlawanan arah jarum jam).
Pada perkalian silang vektor berlaku sifat antikomutatif
d. Letak Kuadran sebuah vektor untuk menentukan θ
sumber : https://www.geschool.net/gebook/84/vektor#imageleft
















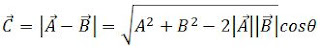




Tidak ada komentar:
Posting Komentar